R ile Çoklu Regresyon Analizi: (Wooldridge Örnekleri)
Çoklu regresyon analizinde bir çok fonksiyonel form kullanılabilir ve bu bize daha fazla esneklik sağlar.
Önceki bölümlerde basit regresyon modeli ele alındı ancak basit regresyon açıklamak istediğimiz bağımlı değişkeni sadece bir bağımsız değişkenle açıklamaya çalıştığı için ceteris paribus (diğer herşey sabitken) varsayımını ihlal etmesi çok olasıydı. Üstelik bu bağımlı değişkeni açıklayan ve bağımlı değişkenin üzerinde de etkisi olan başka bir değişken olmaması olasılığı da çok düşüktü. Çoklu regresyon modeli tahmincimize başka değişkenler ekleyerek y nin üzerindeki varyasyonu daha fazla açıklama şansı doğuracaktır. Çoklu regresyon modelinin bir diğer avantajı bağımsız değişkenin derecelerini arttırarak parametrelerde doğrusal olmasına rağmen doğrusal olmayan fonksiyonlar elde edilebilir ve daha iyi bir açıklayıcı elde edilebilir.
İki bağımsız değişkenli model
Bu bölümün Wooldridge kitabınızda bulunan ilk örnek maaş (wage) bağımlı değişkenin iki bağımsız değişkenle açıklamaya çalıştığımız model. Bu modeli tekrar hatırlayalım.
$$ wage= \beta_0 + \beta_1 educ + \beta_2 exper + u $$
Burada $exper$ iş hayatında ki deneyim yılı, $educ$ eğitim yılını gösteren bağımsız değişkenler, ve $u$ ise gözlemleyemediğimiz diğer faktörler olarak özetlenebilir. Burada basit regresyon modelinde de anlamaya çalıştığımız gibi asıl ilgilendiğimiz parametre $\beta_1$ yani maaşı etkileyen diğer bütün faktörleri sabit tuttuğumuzda eğitimin gelir üzerinde ne kadar bir etkisi olduğu.
Basit regresyon bölümünde kurduğumuz modeli dikkate alalım
$$ wage= \beta_0 + \beta_1 educ + u $$ Burada $\beta_2 exper$ gözlemleyemediğimiz diğer faktörler $u$’nun içindeydi. Çoklu regresyon modelimizde $\beta_2 exper$ terimini $u$’nun içinden çıkarıp modelimize ekleyince en azından deneyimin ($exper$), maaşlar ($wage$) üzerindeki etkisini $\beta_2$ katsayısıyla ölçebileceğiz.
Ancak hala yapmamız gereken önemli varsayımlar mevcut. Bu ikili değişken modelinin bize kattığı artık $\beta_1$ katsayısını en azından deneyimi ($exper$) sabit tutarak ölçebileceğimizi biliyoruz. Basit regresyon modelinde, yani deneyim ($exper$), $u$ teriminin içindeyken, deneyimin, eğitimle bir korelasyonu olmadığını varsaymak zorundaydık. Burada şunu unutmamak gerekir, iki açıklayıcı değişkenli modelde de hala $u$ teriminin içinde bulunan gözlemleyemediğimiz değişkenler, eğitim ($educ$) ve deneyim ($exper$) değişkenleriyle ilgisiz olmalıdır. Bunun sağlanması çok zor olan bir varsayım olduğunu aklınızdan çıkarmayın.
Anlaşıldığı gibi, bu bölüm atlanan (gözlemlenemeyen) değişken sapmasını (“omitted variable bias”) da belli bir ölçüde açıklayacaktır. Çoklu regresyon modelini kullanmamızın bir diğer nedeni de örneğimizden anlaşılacağı üzere gözlemlenemeyen (atlanan) değişken sapmasını ortadan kaldırabilmektir.
Çoklu regresyonun ana fikirlerinden biri, bu ihmal edilen değişkenler hakkında verimiz varsa, onları ek regresörler olarak modele dahil edebilmek ve böylece diğer değişkenleri (deneyim ($exper$) gibi) sabit tutarken bir diğer regresörün (eğitim ($educ$) gibi) bağımsız değişken (maaşlar ($wage$) gibi) üzerindeki nedensel etkisini tahmin edebilmektir.
Alternatif olarak, eğer biri nedensel çıkarımlar değil de tahminle ilgileniyorsa, çoklu regresyon modeli, tek bir regresör kullanılarak yapılan tahminleri geliştirmek için birden fazla değişkenin regresör olarak kullanılmasını mümkün kılar. Bu konuya ilerideki kesimlerde daha detaylı olarak geri döneceğiz.
Kitabınızda sunulan bir diğer iki bağımsız değişkenli regresyon örneği, öğrenci başına yapılan harcamanın ($expend$), lise öğrencilerinin ortalama test sonuçları ($avgscore$) üzerindeki etkisini inceliyor. Örnek olarak şu model kullanılıyor.
$$ avgscore= \beta_0 + \beta_1 expend + \beta_2 avginc + u $$ $avginc$ ailenin ortalama geliri ve $u$ diğer gözlemlenemeyen faktörleri temsil eder. Bulmaya çalıştığımız etki, öğrenci başına yapılan harcamanın ($expend$), lise öğrencilerinin ortalama test sonuçları ($avgscore$) üzerindeki etkisini gösteren $\beta_1$ dir. Ancak ailenin ortalama geliri, harcamalar üzerinde bir etkiye sahip olduğundan, $avginc$ değişkenini regresyona dahil etmemek, en küçük kareler metoduyla bulduğumuz basit regresyon katsayısını ($\beta_1$) sapmalı hale getirecektir.
İki bağımsız değişkenli çoklu regresyon modelini genel bir şekilde yazarsak,
$$ y= \beta_0 + \beta_1 x_1+ \beta_2 x_2 + u $$
Burada,
$\beta_0$ kesen, $\beta_1$ diğer faktörleri sabit tutarak y’deki değişimi x1’e göre ölçer $\beta_2$ diğer faktörleri sabit tutarak y’deki değişimi x2’ye göre ölçer
İki açıklayıcı değişkenli regresyon modelinin kitabınızdaki bir diğer örneği, doğrusal regresyon modelinin fonksiyonel olarak yazılabildiğini göstermek için verilmiştir. Ailenin tüketimini, ailenin gelirinin ikinci dereceden (quadratic) bir fonksiyonu olarak gösterirsek
$$ cons= \beta_0 + \beta_1 inc+ \beta_2 inc^2 + u $$
$cons$ ailenin tüketimi, $inc$ ailenin geliri, $u$ tüketimi etkileyen diğer faktörler olarak özetlenebilir.
k bağımsız değişkenli model
Çoklu regresyon modeli olarak adlandırılabilir.
$$ y= \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + … + \beta_k x_k + u $$
$u$ terimi hata terimi veya gözlenemeyen diğer faktörler olarak adlandırılabilir.
Çoklu regresyon modelinin temel varsayımını hatırlayalım.
$$ E(u | x_1, x_2, x_3,…,x_k)=0 $$ Gözleyemediğimiz diğer faktörlerin, bağımsız değişkenlerle ilişkisiz olması gerektiğini gösteren varsayımdır.
Örnek3.1 Kolej Gpa’sının Belirleyicileri
- ödeviniz olarak da verdiğim kolej Gpa’sının belirleyicileri örneğinin datasını indirelim ve içinde bulunan değişkenlere göz atalım.
library(wooldridge)
data(gpa1)
library(rmarkdown)
paged_table(gpa1)
Örnek için kullanacağımız değişkenlerin tanımlarını şöyle yapabiliriz.
colGPA: MSU GPA, Michigan State Üniversitesi not ortalaması
hsGPA: high school GPA, lise not ortalaması
ACT: ‘achievement’ score, ACT, bir öğrencinin okulda ne öğrendiğini ölçen bir başarı testidir. SAT daha çok bir yetenek testidir, muhakeme ve sözel yetenekleri test eder. Üniversiteler SAT veya ACT sonuçları ile öğrenci kabul eder.
Kitabınızda regresyon sonuçları direk verilen örneğin sonuçlarını bulmak isterseniz şu komutları kullanabilirsiniz.
coklureg <- lm(colGPA~ hsGPA+ACT,data = gpa1)
summary(coklureg)
##
## Call:
## lm(formula = colGPA ~ hsGPA + ACT, data = gpa1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.85442 -0.24666 -0.02614 0.28127 0.85357
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.286328 0.340822 3.774 0.000238 ***
## hsGPA 0.453456 0.095813 4.733 5.42e-06 ***
## ACT 0.009426 0.010777 0.875 0.383297
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3403 on 138 degrees of freedom
## Multiple R-squared: 0.1764, Adjusted R-squared: 0.1645
## F-statistic: 14.78 on 2 and 138 DF, p-value: 1.526e-06
$$ colGPA= 1.29 + 0.453 hsGPA+ 0.0094 ACT + u $$
Peki bu modeli nasıl yorumlayacağız? İlk olarak kesişim katsayısı, hsGPA ve ACT’nin her ikisi de sıfır olursa, öngörülen üniversite GPA’sini göstermektedir ve örneğimizde 1.29 olarak hesaplanmıştır. Üniversiteye giden hiç kimsenin lise not ortalaması sıfır veya başarı testi sıfır olmadığı için, bu denklemdeki kesişim kendi başına anlamlı değildir. Eğim katsayılarına bakınca ikisinin de bekleneceği gibi pozitif olduğunu görüyoruz. Eğer ACT puanını sabit tutarsak, hsGPA’deki 1 birimlik artış colGPA üzerinde 0.453 puanlık bir artış yaratacaktır. Başka bir deyişle, eğer ACT puanları aynı olan iki öğrenci varsa ve bir öğrencinin lise not ortalaması diğer öğrenciden bir puan yüksekse, bu öğrencinin üniversite not ortalamasının yarım puan daha fazla olmasını tahmin edebiliriz.
Üniversite not ortalamalarının 4 üzerinden, ACT sonuçlarının 36 puan üzerinden hesaplandığı düşünülürse, ACT’nin eğimi 0.0094’ün üniversite not ortalaması üzerinde fazla bir etkisi olmadığı düşünülebilir. Hata paylarını göz önüne aldığımızda ACT’nin sadece küçük değil aynı zamanda istatiksel olarak da anlamlı olmadığını göreceğiz.
Basit regresyon örneğimizi hatırlarsak
basitreg <- lm(colGPA~ACT,data = gpa1)
summary(basitreg)
##
## Call:
## lm(formula = colGPA ~ ACT, data = gpa1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.85251 -0.25251 -0.04426 0.26400 0.89336
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.40298 0.26420 9.095 8.8e-16 ***
## ACT 0.02706 0.01086 2.491 0.0139 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3656 on 139 degrees of freedom
## Multiple R-squared: 0.04275, Adjusted R-squared: 0.03586
## F-statistic: 6.207 on 1 and 139 DF, p-value: 0.0139
ACT’nin katsayısı çoklu regresyona göre bir hayli büyük kalıyor (0.02706/0.009426=2.87 kat daha fazla). ACT değerinin çoklu regresyonda lise not ortalaması eklenince azaldığını gözlemliyoruz. Çünkü lise not ortalaması ve ACT arasında yüksek bir korelasyon var. Bu durum bize aslında basit regresyon kullanıldığında temel varsayımı ihlal ettiğimize dair güçlü bir ipucu veriyor.
Bu örnekte son olarak basit ve iki bağımsız değişkenli regresyon grafiklerini gösterelim. Basit regresyon örneğimiz için, dağılım grafiğine bir regresyon çizgisi eklememizin yeterli olduğunu hatırlayalım.
plot(gpa1$ACT,gpa1$colGPA)
abline(basitreg)
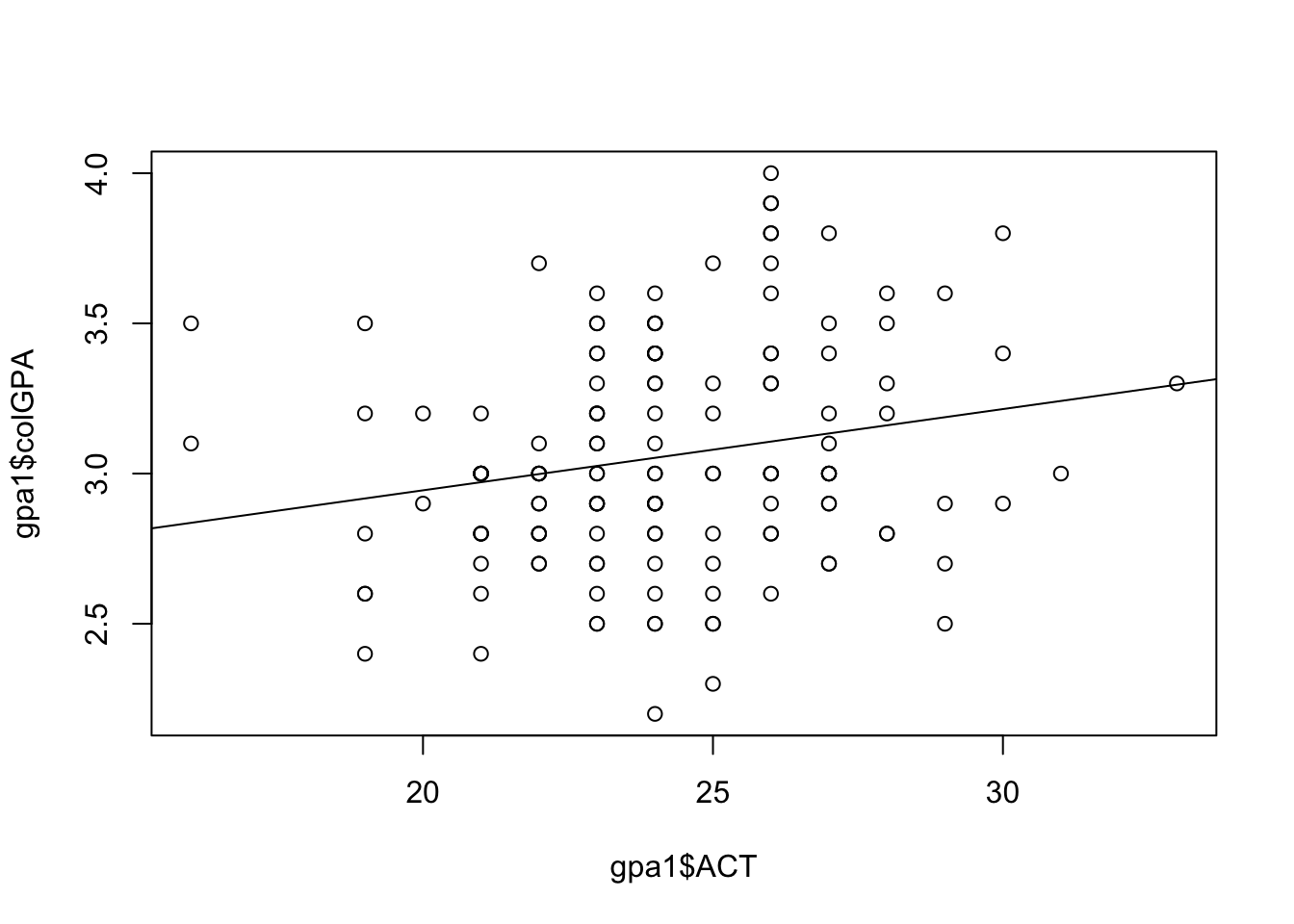Bu grafik sadece iki boyutlu olduğundan, iki boyutlu bilgisayar ekranlarımızda göstermek daha kolaydır. Y eksenine üniversite not ortalaması, X eksenine ACT puanlarını koyuyoruz. Son olarak bulduğumuz eğim ve kesen katsayılarını grafiğimizde temsil eden doğrumuzu çiziyoruz.
Ancak çok değişkenli regresyon grafiklerini, iki boyutlu bilgisayar ekranlarda göstermek biraz daha zor olabilir. En azından örneğimizdeki gibi üç boyutlu bir grafiğe ihtiyacımız var. Önce bütün değişkenler için üç boyutlu bir dağılım grafiği çizelim daha sonra doğru yerine bir düzlem eklememiz gerekecek.
library(plotly)
library(reshape2)
cf.mod <- coef(coklureg)
hsGPA <- seq(min(gpa1$hsGPA),max(gpa1$hsGPA),length.out=50)
ACT <- seq(min(gpa1$ACT),max(gpa1$ACT),length.out=50)
colGPA <- t(outer(hsGPA, ACT, function(x,y) cf.mod[1]+cf.mod[2]*x+cf.mod[3]*y))
p <- plot_ly(x=~hsGPA, y=~ACT, z=~colGPA,type="surface") %>%
add_trace(data=gpa1, x=gpa1$hsGPA, y=gpa1$ACT, z=gpa1$colGPA, mode="markers", type="scatter3d", opacity=0.5)
p
Üç boyutlu grafiğimiz olduğu için artık üzerine gidip sağa sola çevirebilirsiniz. Tahmin edebileceğiniz gibi üç boyutlu grafikleri algılamamız daha büyük boyutlu grafiklerden daha kolay. Şimdi bu noktalarda oluşacak hata payını minimize edecek bir düzleme ihtiyacımız var. Bunun için çoklu regresyonumuzdan yardım alacağız.
Sizin şimdilik bu grafikleri çizerken kullandığımız kodları anlamanıza gerek yok. Sadece grafiklerin şekline odaklanın. Bu grafik bize yapmış olduğumuz minimizasyon işleminin neden basit regresyona bir değişken daha eklediğimizde farklılaştığı ve ek değişkenin toplamda neden daha çok varyasyon açıklamaya yardım ettiği hakkında daha fazla bir içgüdü sunabilir.
Regresyon Tahmin Değerleri ve Hata Payı (OLS Fitted Values and Residuals)
Kitabınızdaki bu bölümde çoklu regresyonda tahmin değerleri ve hata payı üzerinde duruluyor. Tahmin değerlerini şapkayla (hat) gösteriyorduk.
$$ \hat{y_i}= \hat{\beta_0} + \hat{\beta_1} x_{i1} + \hat{\beta_2} x_{i2} + \hat{\beta_3} x_{i3} + … + \hat{\beta_k} x_{ik} $$ Gerçek popülasyon modelimiz ise bu şekilde gösteriliyordu.
$$ y_i= \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i3} + … + \beta_k x_{ik} + u_i $$ Normalde, bir $i$ gözlemi için gerçek değer $y_i$ ve tahmin edilen $\hat{y_i}$ birbirine eşit olmaz. Biz ancak bu hata payını minimize eden en küçük kareler yöntemini kullanarak doğrusal regresyon tahminlerini kullanabiliriz. Bu durumda her bir gözlem için hata payını şu şekilde tahmin edebiliriz.
$$ y_i-\hat{y_i}=\hat{u_i} $$
Çoklu regresyon tahmin değerleri ve hata payının özellikleri.
- Hata payının örnek ortalaması sıfırdır, bu yüzden $\bar{\hat{y}}=\bar{y}$ olur.
- Hata payının herbir bağımsız değişkenle örnek kovaryası sıfırdır. Bu yüzden çoklu regresyon tahmin değerleri ve hata payı arasında örnek kovaryans da sıfırdır.
- Bütün bağımsız değişkenlerin ve bağımlı değişkenin ortalamaları regresyon çizgisi üzerindedir.
$$ \bar{y}= \hat{\beta_0} + \hat{\beta_1} \bar{x_1} + \hat{\beta_2} \bar{x_2} + \hat{\beta_3} \bar{x_3} + … + \hat{\beta_k} \bar{x_k} $$
Çoklu Regresyon Modeli (Multiple Linear Regression (MLR) Model) Varsayımları
- Birinci Varsayım (MLR.1): Parametrelerde doğrusaldır.
$$ y= \beta_0 + \beta_1 x_{1} + \beta_2 x_{2} + \beta_3 x_{3} + … + \beta_k x_{k} + u $$ $\beta$ terimleri doğrusaldır ancak $x$ terimlerinin doğrusal olmasına gerek yoktur. Çoğu zaman $x$ terimlerinin logaritması alınabilir veya $x^2$ gibi fonksiyonal formları kullanılabilir.
- İkinci Varsayım (MLR.2): Rastgele Örnekleme.
Rastgele n örnek gözlemimiz var.
- Üçüncü Varsayım (MLR.3): Mükemmel bir eş doğrusallık yoktur.
Örneklemde (ve dolayısıyla popülasyonda), bağımsız değişkenlerin hiçbiri sabit değildir ve bağımsız değişkenler arasında kesin doğrusal ilişkiler yoktur.
- Dördüncü Varsayım (MLR.4): Sıfır koşullu ortalama.
Modelde bulunan bağımısız değişkenlerin herhangi bir değeri için hata payı $u$’nun koşullu beklenen değeri sıfırdır. $E(u | x_1, x_2, …, x_k) = 0$
Gözlemlenemeyen Değişken Sapması (Omitted Variable Bias)
Gerçek popülasyon modelinde bulunan bir değişkeni modelimize eklememek gözlenemeyen değişken sapmasına yol açabilir. Bu sapmayı kitabınızda verilen örnek üzerinden inceleyeceğiz.
Varsayalım ki maaşları açıklayabilen sadece iki değişkene ihtiyacımız var. Bunlar eğitim ve yetenek. O zaman gerçek popülasyon modelimiz şu şekilde olur.
$$ maaş = \beta_0 + \beta_1 eğitim + \beta_2 yetenek + u $$
Bu modelin bütün çoklu regresyon varsayımlarını (MLR1-MLR4) sağladığını varsayalım. Şimdi yeteneği gözlemleyemediğinizi varsayalım ve sadece, eğitim ve maaş verilerine sahip olduğunuzu düşünün. Sadece basit regresyon modelini kullanabilirsiniz ve $\beta$ katsayılarını tahmin edebilirsiniz. Burda gerçek modeli kullanamadığınız için bu regresyon modelinden elde ettiğimiz tahminleri tilda $\sim$ ile gösterelim.
$$ maaş = \beta_0 + \beta_1 eğitim + v $$
$$ \tilde{maaş} = \tilde{\beta_0} + \tilde{\beta_1} eğitim $$ $v$ hata payı, yetenek gözlenemediği için şu şekilde yazılabilir: $v=\beta_2 yetenek + u$
Eğer $yetenek$ gözlemlenebilseydi şu şekilde tahmin edebilirdik.
$$ \hat{maaş} = \hat{\beta_0} + \hat{\beta_1} eğitim + \hat{\beta_2} yetenek $$ $\hat{\beta_1}$ tahmincisi yetenek değişkenini sabit tutarak bir birim eğitim değişimin maaşı kaç birim değiştireceğini göstermektedir. $\tilde{\beta_1}$ ise bir birim eğitim değişimin maaşı kaç birim değiştireceğini gösterir ancak yetenek değişkenini sabit tutmaz.
Burdan $\tilde{\beta_1}$ sapması şu şekide gösterilebilir
$$ \tilde{\beta_1}= \hat{\beta_1} + \hat{\beta_2} \tilde{\delta_1} $$ $\tilde{\delta_1}$ yeteneğin eğitim üzerindeki basit regresyonunun eğim parametresidir.
$$ \tilde{eğitim} = \tilde{\delta_0} + \tilde{\delta_1} yetenek $$ Eğitim yetenek arttığı için artacağından, yeteneği modele katmamak $\tilde{\beta_1}$ tahmininin o kadar artmasına yol açar.
Şimdi bu hesaplamamızı bir örnek üzerinden gösterelim. Bu örneği hatırlarsak
##install.packages("stargazer")
library(stargazer)
stargazer(list(coklureg,basitreg),type = "text")
##
## =================================================================
## Dependent variable:
## ---------------------------------------------
## colGPA
## (1) (2)
## -----------------------------------------------------------------
## hsGPA 0.453***
## (0.096)
##
## ACT 0.009 0.027**
## (0.011) (0.011)
##
## Constant 1.286*** 2.403***
## (0.341) (0.264)
##
## -----------------------------------------------------------------
## Observations 141 141
## R2 0.176 0.043
## Adjusted R2 0.164 0.036
## Residual Std. Error 0.340 (df = 138) 0.366 (df = 139)
## F Statistic 14.781*** (df = 2; 138) 6.207** (df = 1; 139)
## =================================================================
## Note: *p<0.1; **p<0.05; ***p<0.01
Çoklu regresyon modeli şu şekilde yazılabilir
$$ colGPA = \beta_0 + \beta_1 ACT + \beta_2 hsGPA + u $$ Çoklu regresyonun sonuçları şu şekilde rapor edilebilir
$$ colGPA = 1.286 + 0.009 ACT + 0.453 hsGPA $$ Basit regresyon modeli
$$ colGPA = \beta_0 + \beta_1 ACT + v $$ Basit regresyon modeli sonuçları
$$ colGPA = 2.403 + 0.027 ACT $$ Bu sonuçlar sapmalı sonuçlar olduğu için $\sim$ işaretiyle gösterelim
$$ \tilde{colGPA} = \tilde{\beta_0} + \tilde{\beta_1} ACT $$
Çoklu regresyon modelimiz gerçeğe daha yakın bir model olduğundan tahminleri şapkayla gösteriyoruz.
$$ \hat{colGPA} = \hat{\beta_0} + \hat{\beta_1} ACT + \hat{\beta_2} hsGPA $$ Sapmalı tahminleri bu formülle gösteriyorduk
$$ \tilde{\beta_1}= \hat{\beta_1} + \hat{\beta_2} \tilde{\delta_1} $$ Bütün bildiğimiz değerleri yerine koyarsak
$$ 0.027= 0.009 + 0.453 \tilde{\delta_1} $$ Önce işlemle sonra basit regresyonla sapmayı $\tilde{\delta_1}$ bulalım.
$$ 0.027= 0.009 + 0.453 \tilde{\delta_1}\ \tilde{\delta_1}= \frac{(0.027-0.009)}{0.453}=0.0397 $$ $\tilde{\delta_1}$ iki bağımsız değişkenin birbirleri arasındaki basit regresyon ilişkisinden de bulunabilir
$$ \tilde{ACT} = \tilde{\delta_0} + \tilde{\delta_1} hsGPA $$
sapmareg<-lm(hsGPA~ACT,data = gpa1)
stargazer(list(sapmareg),type = "text")
##
## ===============================================
## Dependent variable:
## ---------------------------
## hsGPA
## -----------------------------------------------
## ACT 0.039***
## (0.009)
##
## Constant 2.463***
## (0.218)
##
## -----------------------------------------------
## Observations 141
## R2 0.120
## Adjusted R2 0.113
## Residual Std. Error 0.301 (df = 139)
## F Statistic 18.879*** (df = 1; 139)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01
Regresyon sonucuyla bulduğumuz ve hesapladığımız $\tilde{\delta_1}$ aynı olduğuna dikkat edin. Basit regresyon yaptığımızda gözlemleyemediğimiz değişken yüzünden olan sapma $\hat{\beta_2} \tilde{\delta_1}=0.453 \cdot 0.0397=0.017$ olur. Bu fark $\tilde{\beta_1}-\hat{\beta_1}$ arasındaki farka eşittir.
Çoklu regresyon (En küçük kareler (OLS)) tahmincilerinin varyansı
Homoskedastisite (Eş varyanslık), Çoklu eşdoğrusallık (Multicollinearity) ve Varyans enflasyon faktörü (Variance inflation factor (VIF))
Çoklu regresyonun 5. varsayımını hatırlayalım.
Beşinci Varsayım (MLR.5): Hata terimi $u$ açıklayıcı değişkenlerin her bir değeri için aynı varyansa sahiptir.
MLR.1 ila MLR.5 arasındaki varsayımlar topluca Gauss-Markov varsayımları olarak bilinir (kesitsel regresyon için).
Bir eğimin varyansını hesaplamak için şu formül kullanılabilir.
$$ var(\hat{\beta_j})=\frac{\sigma^2}{SST_j(1-R_j^2)} $$ $SST_j$’yi hatırlarsak
$$ SST_j = \sum{(x_{ji}-\bar{x_j})^2}=(n-1)(var(x_j)) $$ Bu durumda $var(\hat{\beta_j})$’yi üç parça halinde yazabiliriz.
$$ var(\hat{\beta_j})=\frac{1}{n}\cdot\frac{\sigma^2}{var(x_j)}\cdot\frac{1}{1-R_j^2} $$
Bu formülle birlikte şu çıkarımları yapabiliriz.
- $\frac{1}{n}$ bize n yani gözlem sayısı arttıkça eğimin varyansının azalacağını söyler.
- $\sigma^2$ bize hata teriminin çok fazla değişiklik gösterdiğinde, $\beta$ varyansının artacağını söyler.
- $\frac{1}{var(x_j)}$ bize $x_j$’nin varyansı arttıkça $\beta$ varyansının azalacağını söyler. Bunun nedeni $x_j$’in bu sayede konuyla ilgili daha ilişkili bilgiler sağlayabilecek olmasıdır.
- $\frac{1}{1-R_j^2}$ varyans enflasyon faktörü (Variance inflation factor (VIF)) olarak adlandırılır ve çoklu eşdoğrusallık (Multicollinearity) ölçer. Eğer $x_j$ bağımlı değişkeni diğer regresörlerle çok ilişkiliyse (korelasyon yüksekse) bu $R_j^2$’yi arttırır. $R_j^2$ bire yaklaştıkça $\frac{1}{1-R_j^2}$ paydası sıfıra yaklaşır ve $\frac{1}{1-R_j^2}$ sonsuza yaklaşır. Dolayısıyla $\beta_j$’in varyası çok fazla artar.
Örneğimizi kullanarak bu parçaları çıkaralım.
standarthata<-summary(coklureg)$sigma
standarthata
## [1] 0.3403158
Standart hatayi hesaplamak için sadece sigma komutunu kullanıyoruz. Standart hatayi colGPA örneği için 0.34 olarak hesapladık. $\sigma^2$ yani standart hatanın karesi bize regresyonumuzun hata payının varyansını verecektir.
sigmakare<-standarthata^2
sigmakare
## [1] 0.1158148
Regresörlerimiz arasındaki $R_j^2$ hesaplamak için daha önce hesapladığımız sapmareg’i kullanabiliriz. Bu $R_j^2$ bizim için lise not ortalamasıyla ACT sonuçları arasındaki ilişkiyi gösterecektir. Eğer $R_j^2$ bir’e yakınsa çoklu eş doğrusallık muhtemel olabilir.
Rjkare<-summary(sapmareg)$r.squared
Rjkare
## [1] 0.1195815
İki bağımsız değişkenimizin basit regresyonundan elde ettiğimiz $R_j^2$ yaklaşık olarak yüzde 12’dir.
$\frac{1}{1-R_j^2}$ varyans enflasyon faktörü (Variance inflation factor (VIF))’i hesaplayalım.
VIF<-1/(1-Rjkare)
VIF
## [1] 1.135823
son olarak n’i bulmalıyız.
n<-nobs(coklureg)
n
## [1] 141
son olarak $var(x_j)$’yi bulmamız lazım.
varxj<-var(gpa1$hsGPA)*(n-1)/n
varxj
## [1] 0.1016267
Şimdi formülümüzü kullanarak $var(\hat{\beta_j})$’yi hesaplayabiliriz.
$$ var(\hat{\beta_j})=\frac{1}{n}\cdot\frac{\sigma^2}{var(x_j)}\cdot\frac{1}{1-R_j^2} $$
varbetaj<-(1/n)*(sigmakare/varxj)*VIF
varbetaj
## [1] 0.009180115
$\beta_j$’nin standart hatası $var(\hat{\beta_j})$’nin karaköküdür.
sdbetaj<-varbetaj^0.5
sdbetaj
## [1] 0.09581292
Tablodan hsGPA’in standart hatasına bakarsanız bulduğumuz rakamla aynı olduğunu göreceksiniz.
VIF’i bulmanın kolay bir yolu car paketini yüklemektir.
require(car)
vif(coklureg)
## hsGPA ACT
## 1.135823 1.135823
require komutu paket yükleme komutu (install.packages) ve library komutunun ortak komutu olarak düşünülebilir. Eğer bir paketi daha önce yükleyip yüklemediğinizi hatırlamıyorsanız. require paket yüklenmemişse yükleyecek ve library() yapacaktır. Eğer daha önceden yüklüyse sadece library() yapacaktır. vif() komutu VIF’i regresyonunuz için otomatik olarak hesaplar. 1.1358’in bizim daha önce hesapladığımız VIF değeriyle aynı olduğuna dikkat edin.